Alternative Umschreibung
des Verfahrens:
a/b>0 => a·b>0 |
 |
Erklärung |
|
Das Lösungsverfahren, das wir in diesem Kapitel vorstellen, bestand
darin, dass man:
1. Zuerst mit den Quadrat des Nenners multipliziert
2. Den Bruch kürzt, sodass der Bruch zu einem Produkt wird
Man kann das Verfahren auch verkürzt durch folgenden Satz darstellen:
Ist ein Bruch größer (kleiner) als Null, dann ist auch das
Produkt
aus Zähler und Nenner größer (kleiner) als Null:
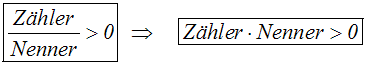 |
|
| |
|
 |
Beweis |
|
Wir beweisen, dass sich der Satz aus dem Lösungsverfahren ergibt,
indem wir es mit einer Bruchungleichung allgemein durchführen.
Gegeben ist eine Bruchungleichung:
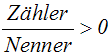
Wir multiplizieren mit dem Quadrat des Nenners:
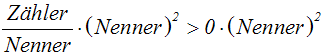
Wir schreiben die linke Seite auf einen Bruchstrich. Die rechte Seite
ist gleich Null:
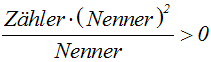
Wir kürzen den Bruch mit dem Nenner:
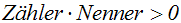
|
|