Bei zwei Brüchen:
Über Kreuz
multiplizieren |
 |
Erklärung |
|
Im vorigen Kapitel haben wir Bruchgleichungen mit dem
"Produkt der Nenner" multipliziert. Besteht eine Bruchgleichung nur
aus zwei Brüchen, dann kann man auch "Über-Kreuz-Multiplizieren".
Unter "Über-Kreuz-Multiplizieren" versteht man dabei eine Regel,
die das "Multiplizieren mit den Produkt der Nenner" und das
anschließende "Kürzen" zu einem Arbeitsschritt zusammenfasst.
Wir betrachten das folgende Beispiel:
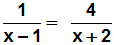
Das "Über-Kreuz-Multiplizieren" funktioniert nun folgendermaßen:
1. Wir multiplizieren den ersten Zähler mit dem zweiten
Nenner.
2. Dann multiplizieren wir den ersten Nenner mit dem zweiten Zähler.
3. Dann setzen wir beide Ergebnisse gleich.
Wir erhalten:
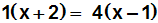
Wir multiplizieren die Klammern aus:
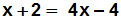
Wir bringen alle x auf die linke Seite, indem wir 4x auf beiden Seiten
subtrahieren:
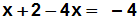
Wir bringen alle Konstanten auf die rechte Seite, indem wir auf beiden
Seiten 2 subtrahieren:
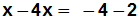
Vereinfachen:
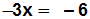
Wir dividieren die Gleichung (also beide Seiten der Gleichung) durch –3:
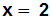
Das Ergebnis liegt im Definitionsbereich, denn der Definitionsbereich
lautet:
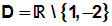
Somit lautet das Ergebnis:
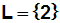 |
|