Verkettung von
Funktionen |
 Definition
Gegeben seien die folgenden zwei Funktionen g und f:
f: x Definition
Gegeben seien die folgenden zwei Funktionen g und f:
f: x 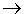 x²
g: x x²
g: x 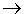 3x
Wendet man auf die Variable x zuerst die Funktion f an, und
danach auf das Ergebnis die Funktion g, so erhält man die
sogenannte Verkettung g(f(x)):
f(x): x 3x
Wendet man auf die Variable x zuerst die Funktion f an, und
danach auf das Ergebnis die Funktion g, so erhält man die
sogenannte Verkettung g(f(x)):
f(x): x 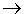 x²
g(f(x)): x x²
g(f(x)): x 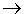 3x²
Man schreibt für die Verkettung g(f(x)) meist kurz: gof
f: x 3x²
Man schreibt für die Verkettung g(f(x)) meist kurz: gof
f: x 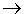 x²
gof: x x²
gof: x 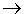 3x²
Man beachte die Reihenfolge: gof bedeutet, daß man auf die
Variable x zuerst die Funktion f und danach die Funktion g
anwendet, und nicht etwa umgekehrt (Näheres siehe unten). 3x²
Man beachte die Reihenfolge: gof bedeutet, daß man auf die
Variable x zuerst die Funktion f und danach die Funktion g
anwendet, und nicht etwa umgekehrt (Näheres siehe unten).
 Sprechweise
Man spricht den Ausdruck gof als: "g nach f" oder "erst f dann g". Sprechweise
Man spricht den Ausdruck gof als: "g nach f" oder "erst f dann g".
 Zwei Anmerkungen zur Definition Zwei Anmerkungen zur Definition
 Man nennt die Funktion f eine unmittelbare Funktion von x und
die Funktion g eine mittelbare Funktion von x. Die Funktion gof
nennt man (wie bereits oben gesagt) die Verkettung von f mit g. Man nennt die Funktion f eine unmittelbare Funktion von x und
die Funktion g eine mittelbare Funktion von x. Die Funktion gof
nennt man (wie bereits oben gesagt) die Verkettung von f mit g.
 Die Verkettung zweier Funktionen ist natürlich auch wieder
eine Funktion. Die Verkettung zweier Funktionen ist natürlich auch wieder
eine Funktion.
 Die Verkettung ist i.Allg. nicht kommutativ
Gegeben seien die beiden Funktionen m und n:
m: x Die Verkettung ist i.Allg. nicht kommutativ
Gegeben seien die beiden Funktionen m und n:
m: x 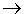 x³
n: x x³
n: x 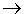 2x
Wir bilden nun die Verkettungen mon und nom:
nom: x 2x
Wir bilden nun die Verkettungen mon und nom:
nom: x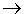 2(x³) = 2x³
mon: x 2(x³) = 2x³
mon: x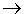 (2x)³ = 8x³
Man sieht: Die Reihenfolge der Verkettung ist im Allg. wichtig.
Leider vertauschen manche Autoren die Reihenfolge, d.h. sie
schreiben für g(f(x)) den Ausdruck fog, anstatt richtig gof. (2x)³ = 8x³
Man sieht: Die Reihenfolge der Verkettung ist im Allg. wichtig.
Leider vertauschen manche Autoren die Reihenfolge, d.h. sie
schreiben für g(f(x)) den Ausdruck fog, anstatt richtig gof.
|