Wurzelfunktionen
mit geradem
Wurzelexponent |
 |
Fall 1: Die Konstante ist positiv |
|
Gegegen ist eine Gleichung, in der eine Wurzelfunktion mit geradem
Exponent vorkommt,
im Beispiel die Quadratwurzelfunktion:
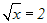
Wir wenden die Quadratfunktion an, d.h. wir quadrieren beide Seiten:
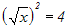
Zuerst überlegen wir uns, ob dies eine Äquivalenz- oder Folgeumformung
ist,
oder eine unerlaubte Umformung:
Der Definitionsbereich der Quadratfunktion ist
R, also größer als der
Wertebereich
der Wurzelfunktion. Die Umformung ist somit eine erlaubte
Umformung, denn es kann
kein unerlaubter Ausdruck entstehen. Allerdings ist die
Quadratfunktion nicht-bijektiv,
und somit handelt es sich um keine Äquivalenzumformung,
sondern um eine
Folgeumformung (Implikation), d.h. wir dürfen am Ende die
Probe nicht vergessen.
Nun wollen wir die linke Seite der Gleichung vereinfachen. Wir überlegen
uns zuerst,
dass x nicht-negativ sein muss, denn wäre x negativ, dann wäre die
Wurzel nicht definiert.
Weil x nicht-negativ ist, dürfen wir das Wurzelgesetz:
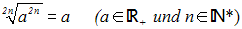
anwenden. Durch diese Termumformung erhalten wir die Gleichung:
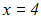
Weil wir eine Folgeumformung vorgenommen haben, müssen wir die Probe
machen.
Die Probe ergibt, dass x=4 eine Lösung der Gleichung ist.
|
 |
Fall 2: Die Konstante ist negativ |
|
Gegegen ist wieder eine Gleichung, in der eine Wurzelfunktion mit geradem
Exponent
vorkommt,
im Beispiel die Quadratwurzelfunktion. Diesmal ist die rechte Seite aber
negativ:
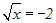
Die Kubikwurzelfunktion können wir nicht anwenden, denn man kann aus
einer negativen
Zahl kein Wurzel ziehen. Damit wir die Kubikwurzelfunktion anwenden
können, müssen
wir daher vorher die Gleichung quadrieren.
Wir wenden die Quadratfunktion an, d.h. wir quadrieren beide Seiten:
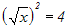
Zuerst überlegen wir uns, ob dies eine Äquivalenz- oder Folgeumformung
ist,
oder eine unerlaubte Umformung. Es gilt wie im Fall oben:
Der Definitionsbereich der Quadratfunktion ist
R, also größer als der
Wertebereich
der Wurzelfunktion. Die Umformung ist somit eine erlaubte
Umformung, denn es kann
kein unerlaubter Ausdruck entstehen. Allerdings ist die
Quadratfunktion nicht-bijektiv,
und somit handelt es sich um keine Äquivalenzumformung,
sondern um eine
Folgeumformung (Implikation), d.h. wir dürfen am Ende die
Probe nicht vergessen.
Nun wollen wir die linke Seite der Gleichung vereinfachen. Wir überlegen
uns zuerst,
dass x nicht-negativ sein muss, denn wäre x negativ, dann wäre die
Wurzel nicht definiert.
Weil x nicht-negativ ist, dürfen wir das Wurzelgesetz:
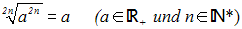
anwenden. Durch diese Termumformung erhalten wir die Gleichung:
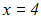
Weil wir eine Folgeumformung vorgenommen haben, müssen wir die Probe
machen.
Die Probe ergibt, dass x=4 keine Lösung der Gleichung ist,
sondern eine Scheinlösung.
|
|