Regeln über die
Zerlegbarkeit
eines Polynoms |
 |
Fall 1: Höchste Potenz ist
eine ungerade Potenz |
|
Nehmen wir an, eine Ungleichung ist in Produktform gegeben.
Dabei sei der Faktor (x5–3x2+1)
noch nicht in Linearfaktoren zerlegt:
(x–1)·(x–2)·(x5–3x2+1)
> 0
Wir fragen uns nun, ob der Faktor zerlegbar ist, oder nicht:
Dann gilt der Satz:
Ist die höchste Potenz in einem Faktor (hier:
x5) eine ungerade Potenz,
so kann mindestens ein weiterer Linearfaktor abgespalten werden. |
In unserem Beispiel ist der Faktor (x5–3x2+1)
also weiter zerlegbar,
denn die höchste Potenz von x ist x5, und 5 ist eine
ungerade Zahl.
Beweis am Ende der Seite
|
 |
Beweis zum Fall 1 |
|
Im Kurs "Polynomfunktionen" haben wir
gelernt:
Der Graph eines Polynoms verläuft für große |x| so wie sein
höchstes Glied,
im Beispiel also wie f(x)=x5.
Im Kurs "Potenzfunktionen" haben wir gelernt, wie f(x)=x5
verläuft:
Eine ungerade Potenzfunktion - wie hier die Funktion
f(x)=x5 -
verläuft im
Koordinatensystem aber von links unten nach rechts oben, und kreuzt daher
auf
jeden Fall die x-Achse, d.h. das Polynom hat eine Nullstelle.
Im Kurs "Polynomgleichungen" haben wir dann gelernt:
Wenn ein Polynom aber eine Nullstelle hat, dann kann man
einen Linearfaktor
abspalten.
Somit ist der Satz von oben bewiesen.
|
 |
Fall 2: Höchste Potenz ist
eine gerade Potenz |
|
Ist in einem Polynom die höchste Potenz
gerade, dann kann man nichts
über die Zerlegbarkeit des Polynoms aussagen. Lediglich Polynome der
folgenden Art sind stets zerlegbar:
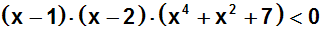
Das Polynom (x4+x2+7) ist nicht zerlegbar, denn
alle Potenzen sind gerade
(und daher nie negativ) und das Absolutglied (7) ist positiv. Daher ist
das
Polynom stets positiv, hat also keine Nullstelle und ist somit nicht
zerlegbar.
I |
| |
|