 Beweisidee
Der Cosinussatz lautete c²=a²+b²-2·a·b·cos Beweisidee
Der Cosinussatz lautete c²=a²+b²-2·a·b·cos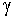
 Wir zeichnen die Höhe h der Seite a ein. Wir zeichnen die Höhe h der Seite a ein.
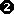 Dadurch können wir c durch h und a1 ausdrücken. Dadurch können wir c durch h und a1 ausdrücken.
 Wir versuchen h und a1 durch die gegebenen Seiten a und b
sowie den gegebenen Winkel Wir versuchen h und a1 durch die gegebenen Seiten a und b
sowie den gegebenen Winkel 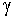 zu ersetzen. zu ersetzen.
 Wir setzen die Ergebnisse von Punkt Wir setzen die Ergebnisse von Punkt  in Punkt in Punkt  ein. ein.
 Details zum Beweis
zu Details zum Beweis
zu  Im unteren rechtwinkligen Dreieck gilt der Satz des
Pythagoras: c² = h² + a1²
zu Im unteren rechtwinkligen Dreieck gilt der Satz des
Pythagoras: c² = h² + a1²
zu  Nun müssen wir in c² = h² + a1² die Seiten
h und a1 durch die Seiten a und b und den
Winkel Nun müssen wir in c² = h² + a1² die Seiten
h und a1 durch die Seiten a und b und den
Winkel 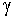 ersetzen. Zuerst ersetzen wir h:
h = sin ersetzen. Zuerst ersetzen wir h:
h = sin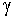 ·b
Als zweites ersetzen wir a1:
a1 = a - a2
a1 = a - (cos ·b
Als zweites ersetzen wir a1:
a1 = a - a2
a1 = a - (cos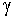 ·b) weil: cos ·b) weil: cos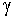 = a2:b)
zu = a2:b)
zu  Schritt 4 besteht nur aus technischen Umformungen:
Wir setzen die Ergebnisse aus 3 in die Formel aus
Punkt 2 ein und multiplizieren die Klammern aus:
c² = (sin Schritt 4 besteht nur aus technischen Umformungen:
Wir setzen die Ergebnisse aus 3 in die Formel aus
Punkt 2 ein und multiplizieren die Klammern aus:
c² = (sin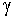 ·b)² + (a - cos ·b)² + (a - cos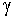 ·b)²
c² = sin² ·b)²
c² = sin²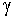 ·b² + a² -2·a·cos ·b² + a² -2·a·cos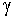 ·b + cos² ·b + cos²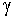 ·b²
Aus dem 1. und 4. Summanden können wir b² ausklammern:
c² = b²(sin² ·b²
Aus dem 1. und 4. Summanden können wir b² ausklammern:
c² = b²(sin²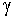 +cos² +cos²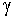 ) + a² -2·a·cos ) + a² -2·a·cos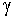 ·b
Die Klammer fällt weg (trigonometrischer Pythagoras).
Diese letzte Umformung ergab den Cosinussatz:
c² = a² + b² -2·a·b·cos ·b
Die Klammer fällt weg (trigonometrischer Pythagoras).
Diese letzte Umformung ergab den Cosinussatz:
c² = a² + b² -2·a·b·cos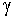
|