x³ > –a
(a nicht-negativ,
d.h. –a sei negativ) |
 |
Lösungsverfahren 1 |
|
Gegeben ist eine Potenzungleichung mit ungeradem Exponent:
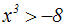
Wären beide Seiten der Ungleichung stets negativ, dann dürften wir die
Umkehrfunktion für ungerade Potenzfunktionen und negative x anwenden.
Die linke Seite der Ungleichung kann sowohl positiv oder negativ
werden.
Wir müssen daher eine Fallunterscheidung machen:

Die Lösungsmenge ist die Vereinigungsmenge beider Fälle, also: L={x|x > –2} |
 |
Lösungsverfahren 2 |
|
Gegeben ist wieder die Potenzungleichung mit ungeradem Exponent von oben:
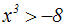
Anstatt jedoch wie oben die Umkehrfunktion zu verwenden, wird im Fall 2
quadriert.

Die Lösungsmenge ist die Vereinigungsmenge beider Fälle, also: L={x|x > –2} |
| |
|