Differenz aus gerader und ungerader Funktion
|
 | Satz |
| Die
Differenz aus einer geraden und einer ungeraden Funktionen ergibt eine Funktion, die zwar
weder gerade noch ungerade ist, doch sie kann
zu anderen
Punkten (bzw. zu Parallelen der y-Achse) symmetrisch sein. |
Beispielsweise besteht die folgende Differenz f(x) aus einer geraden und einer
ungeraden Teilfunktionen, denn g(x)=x4 ist gerade und u(x)=sin(x) ist ungerade:
f(x) = x4
– sin(x)
|
 | Beweis
Teil 1 |
| Im
ersten Teil beweisen wir, dass die Differenz aus gerader und ungerader
Funktion
weder gerade noch ungerade ist.
Gegeben sei also eine Differenz f(x), die aus einer geraden und einer
ungeraden Teilfunktion besteht, die wir g(x) und u(x) nennen:
f(x) = g(x) – u(x)
Wie immer besteht die Beweisidee darin, f(–x) zu berechnen. Dazu ersetzen
wir auf beiden Seiten der Gleichung alle x durch –x:
f(–x) = g(–x) – u(–x)
Die Teilfunktion g(x) ist sind laut Voraussetzung eine gerade Funktion.
Daher dürfen wir g(–x) durch g(x) ersetzen:
f(–x) = g(x) – u(–x)
Die Teilfunktion u(x) ist sind laut Voraussetzung eine ungerade Funktion.
Daher dürfen wir u(–x) durch –u(x) ersetzen:
f(–x) = g(x) – [–u(x)]
Wir lösen die eckige Klammer auf:
f(–x) = g(x) + u(x)
Nun vergleichen wir die rechte Seite der Gleichung mit der ursprünglichen Gleichung:
Die rechte Seite entspricht weder f(x) noch –f(x).
Daher ist die Funktion weder gerade noch ungerade.
|
 | Beweis
Teil 2 |
| Im
ersten Teil haben wir bewiesen, dass die Differenz aus gerader und ungerader
Funktion
weder gerade noch ungerade sein kann.
Im zweiten Teil beweisen wir, dass die Differenz aus gerader und ungerader
Funktion
andere Symmetrien aufweisen kann, oder aber ganz unsymmetrisch ist.
Dazu müssen wir je ein Beispiel angeben können. Ein Beispiel ist die
Funktion:
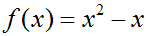
Sie hat einen geraden und einen ungeraden Summanden, und sie ist
symmetrisch
zur Achse x= 0.5, was man durch den Test aus Kapitel 1 beweisen kann:
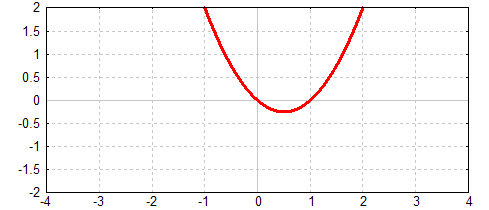
Betrachten wir nun die Funktion:
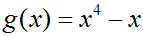
Sie hat ebenfalls einen geraden und einen ungeraden Summanden, ist aber
vollkommen unsymmetrisch:
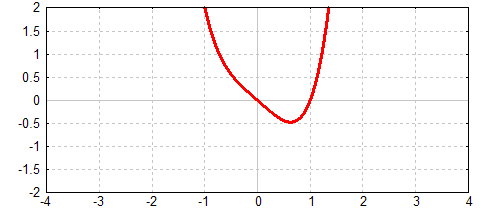
|
| Copyright by www.mathematik.net |
|