 |
Motivation |
|
Wir lernten bereits: Bei Gleichungen ist das Anwenden einer
injektiven Funktion
eine ─quivalenzumformung.
Im Falle einer Ungleichung ist nur das Anwenden einer streng
monotonen Funktion
eine ─quivalenzumformung, und au▀erdem muss man beim Anwenden einer
streng
monoton fallenden Funktion das Ungleichheitszeichen umdrehen.
Wir halten dies in einem Satz fest. |
| |
 |
Satz |
|
Wenn man beide Seiten einer Umgleichung zum Argument einer
streng monoton
steigenden Funktion macht, dann ist dies eine
─quivalenzumformung.
Wenn man beide Seiten einer Umgleichung zum Argument einer
streng monoton
fallenden Funktion macht, dann ist dies eine
─quivalenzumformung,
wenn man das Ungleichheitszeichen umdreht. |
|
| |
 |
Beispiel 1: Streng monoton
steigende Funktion |
|
Gegeben ist die Ungleichung:
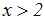
Wir machen beide Seiten zum Argument der Kubikfunktion (=Potenzfunktion
mit dem
Exponenten 3). Weil die Kubikfunktion streng monoton steigend ist,
handelt es sich um
eine ─quivalenzumformung:
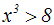
|
 |
Beispiel 2: Streng monoton
fallende Funktion |
|
Gegeben ist die Ungleichung:
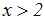
Wir machen beide Seiten zum Argument der Exponentialfunktion mit der
Basis 1/2.
Weil diese Gunktion streng monoton fallend ist, handelt es sich um eine
─quivalenzumformung,
jedoch mŘssen wir gleichzeitig das Ungleichheitszeichen umdrehen:
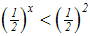
|